Phân phối phương thức (Dispatch) trong Julia

Hàm và Phương thức trong Julia

Trong Julia, ta có khái niệm hàm (functions) và phuơng thức (methods). Hàm đơn giản chỉ là 1 cái tên như: push! hay read. Phương thức là định nghĩa cụ thể của một hàm cho các kiểu đối số (types of arguments) nhất định, ví dụ như push!(s::Set, x) hoặc read(io::IO). Đứng từ góc nhìn hướng đối tượng (object-oriented) bạn có thể xem các phương thức như là các thể hiện (instances) của hàm.

Phân phối phương thức (dispatch)

Như vậy, mỗi khi trình biên dịch (compiler) Julia bắt gặp một hàm, nó sẽ xem xét kiểu (type) của các đối số và chọn phương thức phù hợp nhất để thực thi. Quá trình đó được gọi là phân phối phương thức, hay gọi tắt là phân phối (dispatch). Đây là một khái niệm quan trọng trong Julia, nó cho phép bạn viết mã (code) một cách tự nhiên và hiệu quả.

Đối với bất kì phương thức cho trước nào, bạn có thể xem việc phân phối (dispatch) như là việc cắt ra (slicing) một phần từ không gian các kiểu khả dĩ (possible type space) của hàm đó ứng với một tập hợp các đối số nhất định (trong định nghĩa của hàm đó). Nếu bạn tăng số lượng đối số trong định nghĩa hàm, thì tức là bạn đang thêm nhiều chiều vào không gian kiểu. Xem hình minh hoạ dưới đây:

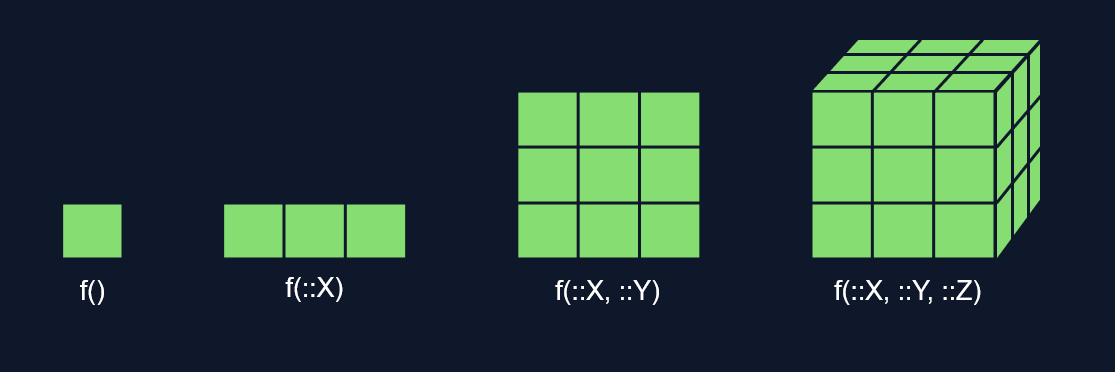
Ví dụ, xét hàm f. Giả sử chỉ có 3 kiểu trong toàn bộ vũ trụ kiểu (type universe) của Julia: Float64, Int64, và String. Float64 và Int64 là các kiểu con (subtype) của Number. Mặc định trong Julia, nếu bạn không chỉ định (specify) kiểu cho đối số nào đó của hàm, thì đối số đó sẽ được giả định là có kiểu Any. Tất cả các kiểu khác đều là kiểu con của Any.

Một phương thức như f(::Any, ::Any) mô tả toàn bộ không gian của tất cả các kiểu khả dĩ cho hàm có tên là f. Ngược lại, một phương thức như f(::Int64, ::String) thì cực kì cụ thể, nó là một điểm duy nhất trong không gian kiểu (điểm - là cách nói thường thấy trong bối cảnh toán học, trên không gian đã đánh toạ độ. Còn trong minh hoạ này, no tương ứng với một ô màu trong biểu đồ minh hoạ dưới đây).

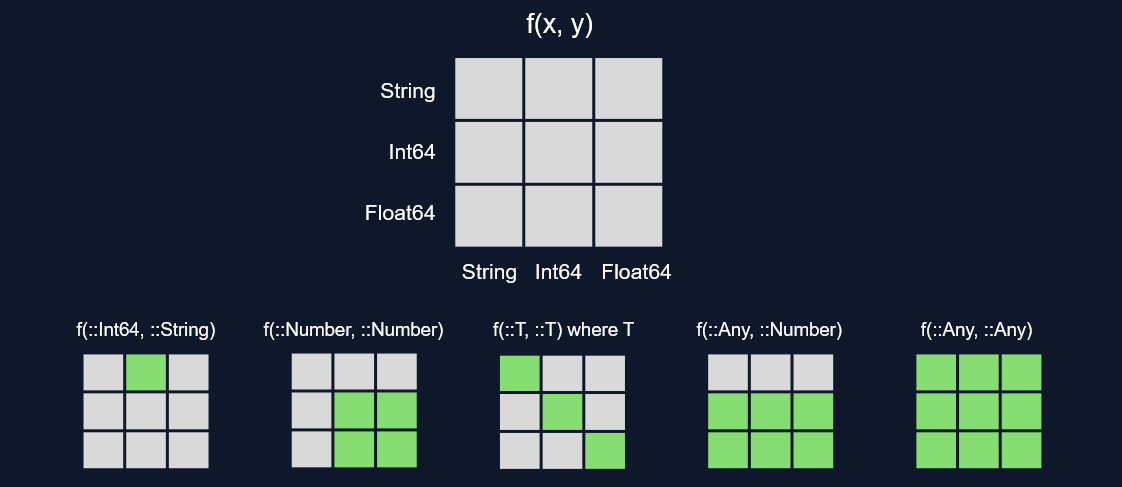
Bạn có thể sử dụng các kiểu trừu tượng (abstract types) như Number hoặc các hợp kiểu (unions) như Union{Float64, Int64} để bao quát một tập hợp con của không gian kiểu rời rạc. Bằng cách này, bạn có thể chọn một phần của không gian mà bạn muốn định nghĩa cho hàm. Trong quá trình chạy (runtime), Julia sẽ phân phối (dispatch) phương thức phù hợp cho hàm ứng với phần không gian kiểu con mà bạn đã chọn trước đó. Các kiểu trừu tượng trong Julia chỉ tồn tại cho mục đích chọn phương thức trên một tập hợp kiểu con, và chúng không có ảnh hưởng nào khác lên chính các kiểu con đó.

Phân phối chéo (diagonal dispatch)

Nếu bạn không biết phân phối chéo (diagonal dispatch) là gì, thì có thể xem minh hoạ dưới đây. Phân phối chéo xảy ra khi kiểu của tất cả các đối số bị ép buộc phải giống với f(::T, ::T) where T. Và định nghĩa này tương ứng với chéo xuyên qua không gian kiểu. Bạn cũng có thể giới hạn phân phối chéo vào một tập con với f(::T, ::T) where T<:Number và trong các không gian nhiều chiều hơn, bạn có thể định nghĩa phức tạp hơn như f(::T, ::T, ::S) where {T<:Number, S<:AbstractString} bằng cách thêm nhiều tham số kiểu (parametric types).

Mức độ ưu tiên trong phân phối phương thức

Khi bạn định nghĩa một phương thức hai lần, bạn cần biết rõ lúc nào thì phương thức nào sẽ được chọn. Trình biên dịch sẽ ưu tiên phương thức nào cụ thể hơn, nghĩa là phương thức nào có khai báo kiểu rõ ràng hơn. Trong hình dưới đây, các phương thức được sắp xếp theo mức độ cụ thể giảm dần từ trái qua phải.

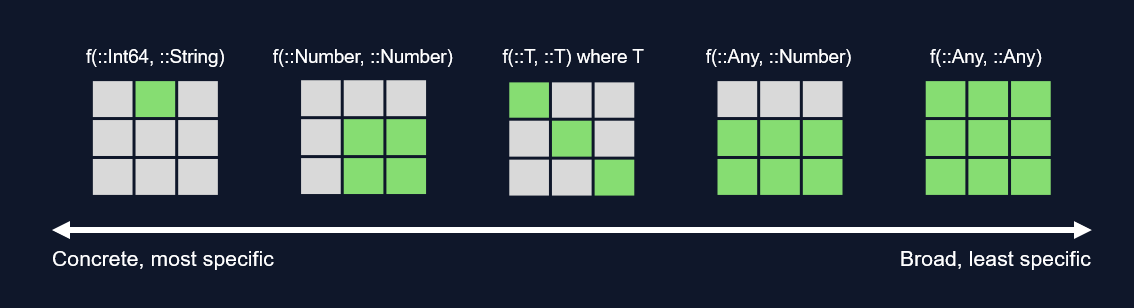
Ví dụ, nến bạn định nghĩa phương thức f như sau:

1
2

f(::Any, ::Any) = println("any & any")
f(::Int64, ::Int64) = println("int & int")

Phần lớn các lần gọi hàm sẽ được phân phối về phương thức chung nhất vì phương thức đó được định nghĩa cho toàn bộ không gian kiểu. Nhưng khi bạn nhập hai số nguyên, trình biên dịch sẽ phân phối về phương thức cụ thể f(::Int64, ::Int64). Ta có thể kiểm tra trong Julia như sau:

1
2
3
4
5

julia> f("string", 5)
any & any

julia> f(4, 5)
int & int

Từ góc nhìn trực quan, chúng ta đã tạo ra một cơ chế phân phối chồng lấp (overlapping dispatch), trong đó có một phương thức được định nghĩa riêng cho trường hợp số nguyên f(::Int64, ::Int64) và được phân phối đến chỉ khi các đối số của hàm là các số nguyên.

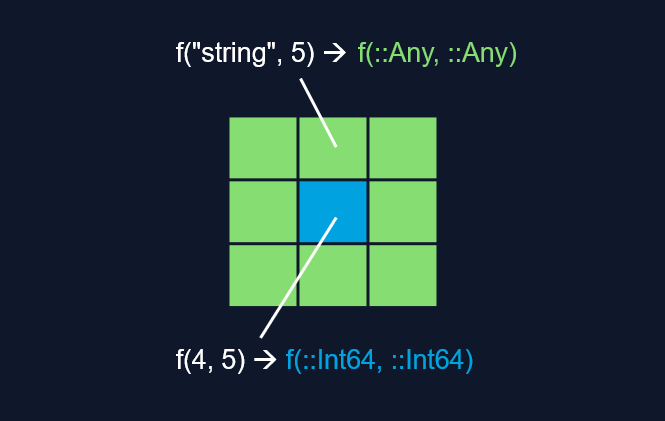
Các phương thức nhập nhằng

Có một số điểm cần lưu ý ở đây. Nếu bạn không cẩn thận, các phương thức có thể trở nên nhập nhằng (ambigous) và Julia sẽ báo lỗi. Ví dụ, nếu bạn định nghĩa như sau:

1
2

f(::Any, ::String) = println("any & string")
f(::String, ::Any) = println("string & any")

Khi đó hàm f("string", "string") sẽ được phân phối cho phương thức nào trong 2 cái trên?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

julia> f("string", 5)
string & any

julia> f(5, "string")
any & string

julia> f("string", "string")
ERROR: MethodError: f(::String, ::String) is ambiguous.  Candidates:
  f(::Any, ::String) in Main at REPL[8]:1
  f(::String, ::Any) in Main at REPL[9]:1
Possible fix, define
  f(::String, ::String)

May mắn là có một cách khắc phục được lỗi đó. Đó là định nghĩa cho trường hợp nhập nhằng. Ban đầu có sự nhầm lẫn vì hai cách dispatch chồng lấp và không cái nào cụ thể hơn cái còn lại. Ta có thể khắc phục bằng cách định nghĩa một phương thức cụ thể hơn trong khu vực xung đột.

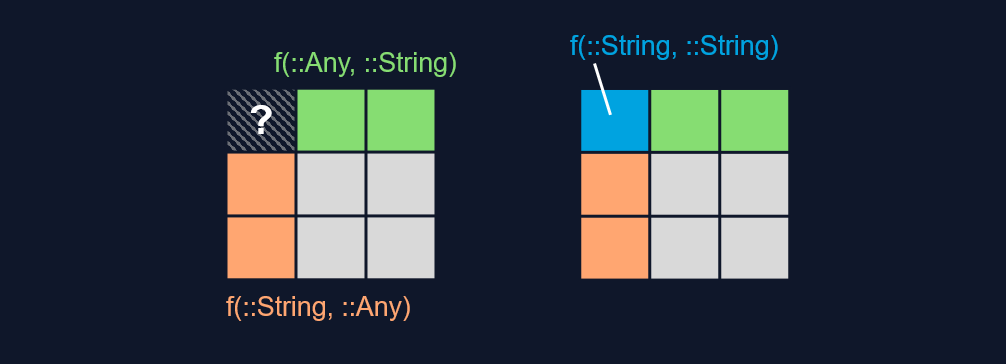
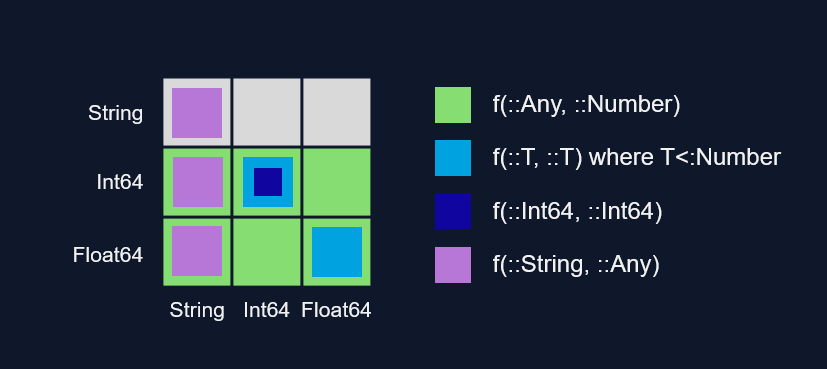
Khi bạn định nghĩa nhiều phương thức, bạn đang tạo ra một bức tranh đầy màu sắc trong không gian kiểu của hàm. Bạn có thể sáng tạo ra những thiết kế độc đáo nhất trong các phương thức của mình, nhưng hãy cẩn thận. Tìm được sự cân bằng hợp lí giữa một vài phương thức trừu tượng lớn và rộng so với nhiều phương thức cụ thể nhỏ là một nghệ thuật thực sự trong Julia.

Mọi người thường không chia sẻ cách họ hình dung thiết kế mã (code) trong tâm trí, trong khi tôi tin rằng điều này thực sự định hình quá trình sáng tạo. Hình ảnh gần nhất với thiết kế mã trong Julia mà tôi đã thấy là bài viết về cách dispatch của Julia với các loại Pokemon. Bạn có thể đọc bài viết đó để xem các ví dụ chi tiết hơn về cơ chế dispatch đa chiều của Julia.

Tham khảo

• https://scientificcoder.com/the-art-of-multiple-dispatch