Tích phân từng phần - làm sao cho đỡ rối
Ý tưởng
Ý tưởng của tích phân từng phần (integration by parts) bắt nguồn từ đạo hàm của một tích.
Nhắc lại, để tính đạo hàm của một tích hai hàm $u$ và $v$, ta sử dụng phương pháp “chia để trị” như sau
$$(uv)' = u'v+uv',\qquad\qquad(1)$$hay, ở dạng khác là
$$\dfrac{d}{dx}(uv) = \dfrac{du}{dx}v + u\dfrac{dv}{dx}.\qquad\qquad(2)$$Nhân cả 2 vế của phương trình (2) với $dx$, ta được
$$d(uv) = u\,dv + v\,du.\qquad\qquad(3)$$Lấy tích phân cả hai vế của phương trình (3) theo biến $x$, ta được
$$\int d(uv) = \int u\,dv + \int v\,du,$$hay
$$uv = \int u\,dv + \int v\,du,$$và chuyển vế qua lại một chút, ta được công thức tích phân từng phần quen thuộc như sau
$$\int {\color{red}u}\,{\color{green}dv} = uv - \int {\color{green}v}\,{\color{red}du}.\qquad\qquad(4)$$Về bản chất, với công thức (4), thay vì đi giải bài toán tích phân ở vế trái $(\int {\color{red}u}\space{\color{green}dv}),$ ta sẽ chuyển sang giải bài toán tích phân ở vế phải $(\int {\color{green}v}\space{\color{red}du}).$ Dĩ nhiên, ta sẽ cần đủ khéo léo để bài toán tích phân mới này phải dễ giải hơn bài toán cũ. Và việc đó phụ thuộc vào cách chúng ta chọn hàm $\color{red}u$ và $\color{green}dv$.
Chọn hàm $\color{red}u$ và $\color{green}dv$ như thế nào?
Hàm $\color{red}u$ ở vế trái sẽ thành $\color{red}du$ ở vế phải. Vì vậy, chúng ta chọn hàm $\color{red}u$ sao cho $\color{red}du$ của nó dễ tính hơn $\color{red}u$.
Hàm $\color{green}dv$ ở vế trái sẽ thành $\color{green}v$ ở vế phải. Thường thì nguyên hàm $\color{green}v$ sẽ không đơn giản hơn $\color{green}dv$. Do đó ta thường không cần cân nhắc gì nhiều ở hàm $\color{green}dv$. Chọn sao mà ta có thể tính được nguyên hàm của hàm $\color{green}dv$ là được. Thường thì các hàm sau sẽ được chọn làm $\color{green}dv$:
Quy tắc LIATE
- L - Logarit (hàm logarit): $\ln(x), \log_b(x), \dots$
- I - Inverse trigonometric functions (hàm lượng giác ngược): $\arctan(x), \arcsin(x), \dots$
- A - Algebraic functions (hàm đa thức): $x^n, \sqrt{x}, \dots$
- T - Trigonometric functions (hàm lượng giác): $\sin x, \cos x , \tan x , \dots$
- E - Exponential functions (hàm mũ): $e^x, 19^x, \dots$
Để ý sẽ thấy các hàm ở phía dưới danh sách thường có nguyên hàm đơn giản hơn so với các hàm phía trên. Vậy nên, nếu có nhiều lựa chọn, ta nên ưu tiên chọn hàm ở phía dưới.
Múa cột!
$$\int x^2.\sin{x}\space dx \qquad\quad\text{(5)}$$Bằng kinh nghiệm vừa đề cập ở trên, ta chọn
$$\color{red}u = x^2,\qquad\qquad\color{green}dv = \sin{x}dx.$$Khi đó:
$$\color{red}du = 2x\,dx,\qquad\qquad\color{green}v = -\cos{x}.$$Áp dụng công thức (4), ta được
$$\int x^2.\sin{x}\space dx = -x^2\cos{x} - \int -2x\cos{x}\space dx + C_1.$$Bài toán tích phân mới lúc này là $\int -2x\cos{x}\space dx.$ Và đúng là nó đơn giản hơn bài toán gốc một chút. Chúng ta có thể áp dụng công thức tích phân từng phần một lần nữa để giải bài toán này. Nhưng lúc này, ta chọn
$$\color{red}u = -2x,\qquad\qquad\color{green}dv = \cos{x}dx.$$Khi đó:
$$\color{red}du = -2\,dx,\qquad\qquad\color{green}v = \sin{x}.$$Áp dụng công thức (4) một lần nữa, ta được
$$\int -2x\cos{x}\space dx = -2x\sin{x} - \int -2\sin{x}\space dx + C_2.$$Bài toán tích phân mới lúc này là $\int -2\sin{x}\space dx.$ Đây là một bài toán dễ dàng hơn nhiều so với bài toán vừa trên. Tính nguyên hàm, ta được
$$\int -2\sin{x}\space dx = 2\cos{x} + C_3.$$Kết hợp với công thức tích phân từng phần, ta có
$$\int x^2.\sin{x}\space dx = -x^2\cos{x} + 2x\sin{x} + 2\cos{x} + C.$$Vậy “múa cột” chỗ nào?
Thực ra, đó là một cách “chơi chữ” của phương pháp sau:
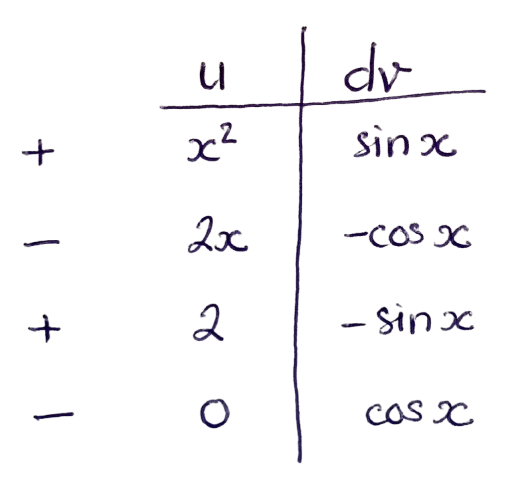
Kẻ 1 cột ngăn cách $\color{red}u$ và $\color{green}dv$. Trên cột $\color{red}u$, ta tiến hành đạo hàm liên tục cho đến khi nó bằng 0. Trên cột $\color{green}dv,$ ta tiến hành tích phân liên tục cho đến hàng có hàm $\color{red} u$ là 0 (Luu ý, để đơn giản, ta đã lược bỏ $dx$). Bổ sung thêm 1 cột phụ bên trái, lần lượt đánh dấu xen kẽ $(+)$ và $(-)$ đến hàng cuối cùng.
Từ trên xuống, đi theo hướng các mũi tên sau, ta sẽ thu được kết quả
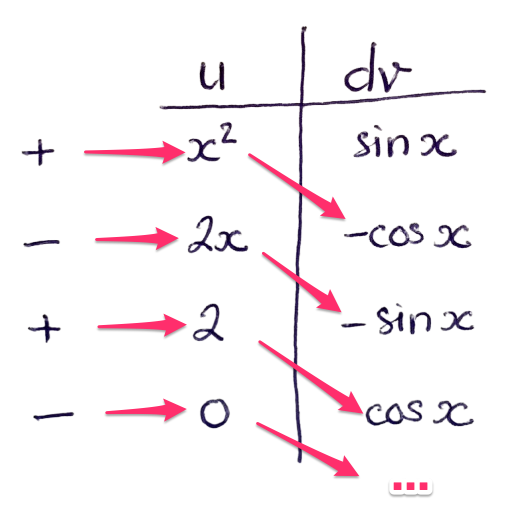
Câu hỏi: Liệu bạn có đoán (hoặc thậm chí chứng minh được) vì sao phương pháp “múa cột” lại cho ra kết quả đúng không? 😗😗😗
Mở rộng
Với một số bài toán như $\int e^{2x}.\sin x\space dx$, cột sẽ dài xuống… vô tận, bạn sẽ phải múa cột quài quài luôn!

Với một chút tinh ý, bạn sẽ nhận ra rằng hàng đầu tiên chính là bài toán tích phân gốc. Các hàng tiếp theo lần lượt là các bài toán tích phân mới khi áp dụng công thức (4). Mặc dù cột kéo dài vô tận, nhưng với bài toán này, hàng thứ 3 đã cho ta cùng bài toán tích phân với bài toán gốc (bỏ qua sự khác biệt không đáng kể về dấu và hằng số). Vậy nên, thực ra, ta chỉ cần múa cột đến hàng thứ 3 là đủ. Tức là
Dựa vào các mũi tên, ta có thể viết như sau:
Đặt $\color{blue}I = \int e^{2x}.\sin x\space dx$, (6) trở thành
$${\color{blue}I} = -e^{2x}.\cos x + 2e^{2x}.\sin x - 4{\color{blue}I} + C_1,$$hay
$$5{\color{blue}I} = -e^{2x}.\cos x + 2e^{2x}.\sin x + C_1,$$và do đó
$${\color{blue}I} = -\dfrac{1}{5}e^{2x}.\cos x + \dfrac{2}{5}e^{2x}.\sin x + \dfrac{C_1}{5},$$hay viết đẹp hơn là
$${\color{blue}\int e^{2x}.\sin x\space dx} = -\dfrac{1}{5}e^{2x}.\cos x + \dfrac{2}{5}e^{2x}.\sin x + C.$$