Tốc độ tiến về vô cùng

Trong nhiều bài toán giải tích, ta thường quan tâm đến tốc độ tiến về vô cùng (còn gọi là tốc độ tăng trưởng) của các hàm số trên đoạn $[0, +\infty)$. Nó liên quan trực tiếp đến sự hội tụ của dãy hay chuỗi, và đóng vai trò quan trọng trong việc chứng minh các định lý quan trọng.

Các hàm thường gặp

Trong bài viết này, ta sẽ so sánh tốc độ tăng trưởng của một số dạng hàm quen thuộc sau:

1. Hàm logarit

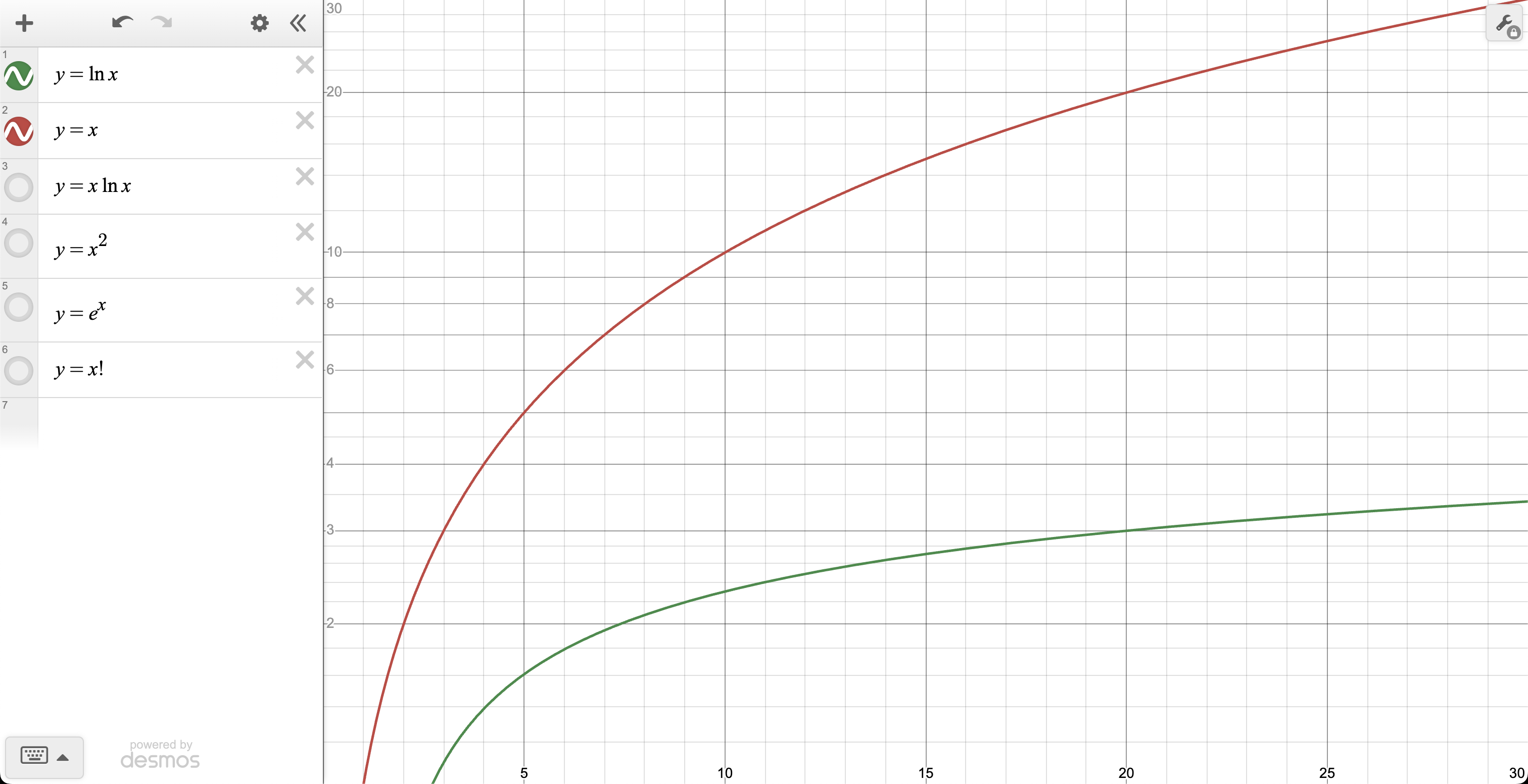
Hàm logarit tự nhiên, $\ln(x)$, tăng rất chậm khi $x \to +\infty$. Giá trị của $\ln(x)$ chỉ tăng thêm một lượng nhỏ ngay cả khi $x$ tăng rất lớn, khiến nó trở thành một trong những hàm có tốc độ tăng trưởng chậm nhất.

Để tiện so sánh với các hàm có tốc độ tăng trưởng rất nhanh trong phần sau, ta sẽ chuyển thang đó của $y$ thành logarit, ta được đồ thị mới như sau:

4. Hàm $y = x \ln x$

Hàm $x \ln x$ kết hợp tốc độ tăng trưởng của $x$ và sự chậm chạp của $\ln(x)$. Mặc dù nó tăng nhanh hơn $\ln(x)$.

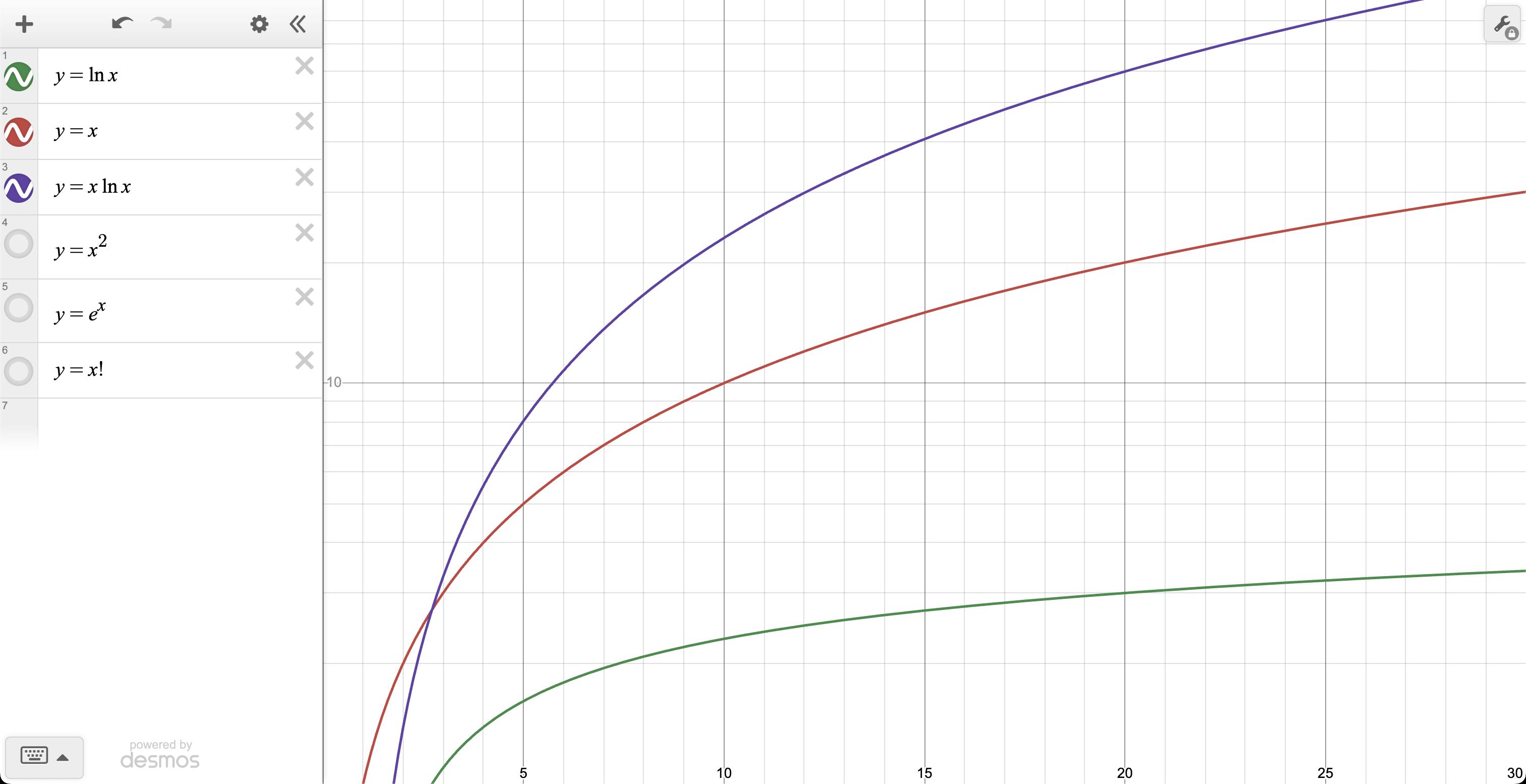
2. Hàm đa thức

Hàm đa thức dạng $P(x) = x^n$, với $n$ là số mũ, có tốc độ tăng trưởng nhanh hơn $x$ và $\ln(x)$.

3. Hàm mũ

Hàm mũ $e^x$ có tốc độ tăng trưởng nhanh hơn đáng kể so với hàm đa thức.

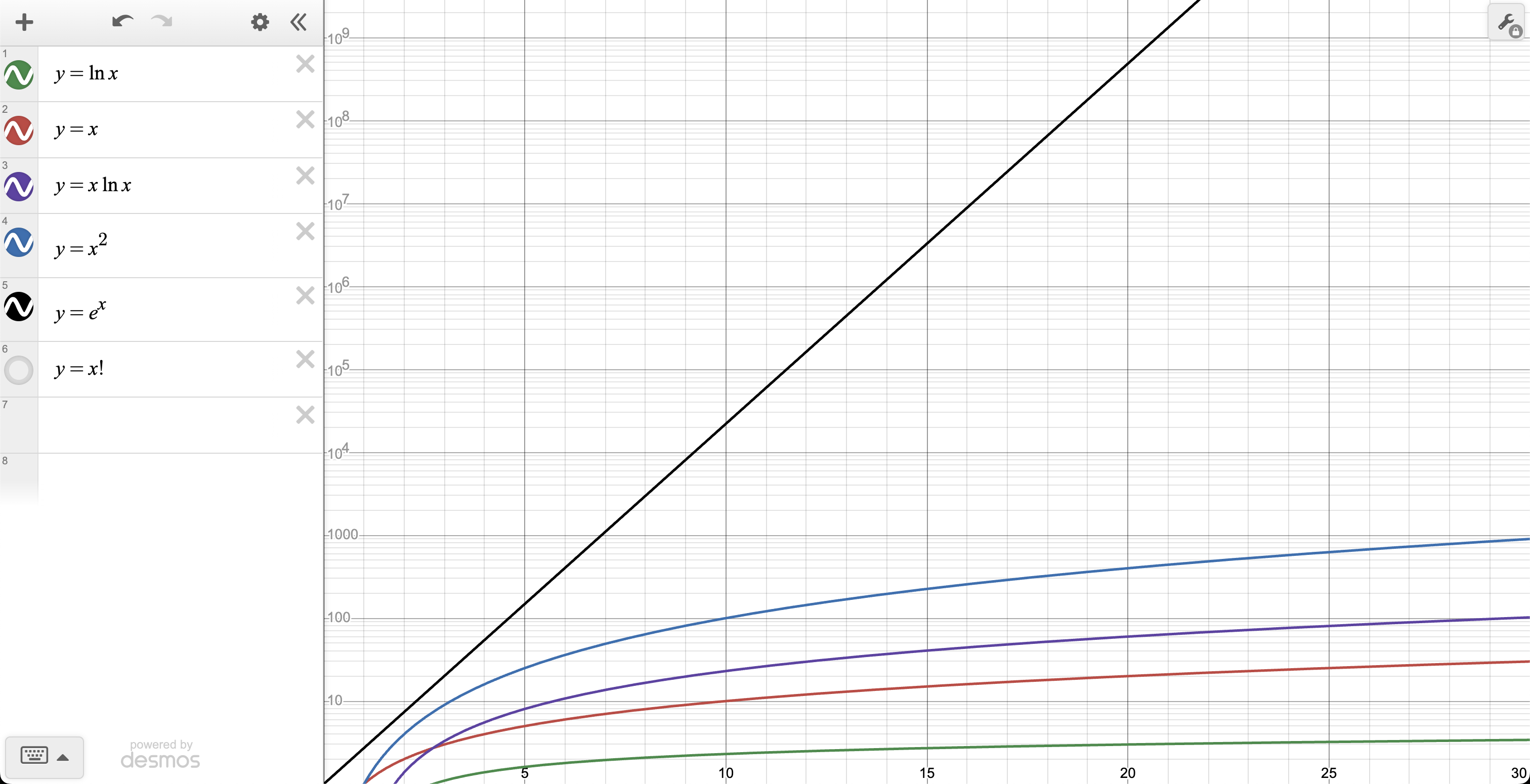
5.Hàm giai thừa

Hàm giai thừa $n!$ được định nghĩa là tích của tất cả các số nguyên từ $1$ đến $n$. Tốc độ tăng trưởng của $n!$ vượt xa cả hàm mũ, bởi vì mỗi lần tăng $n$, ta nhân thêm một số nguyên lớn hơn tất cả các số trước đó.

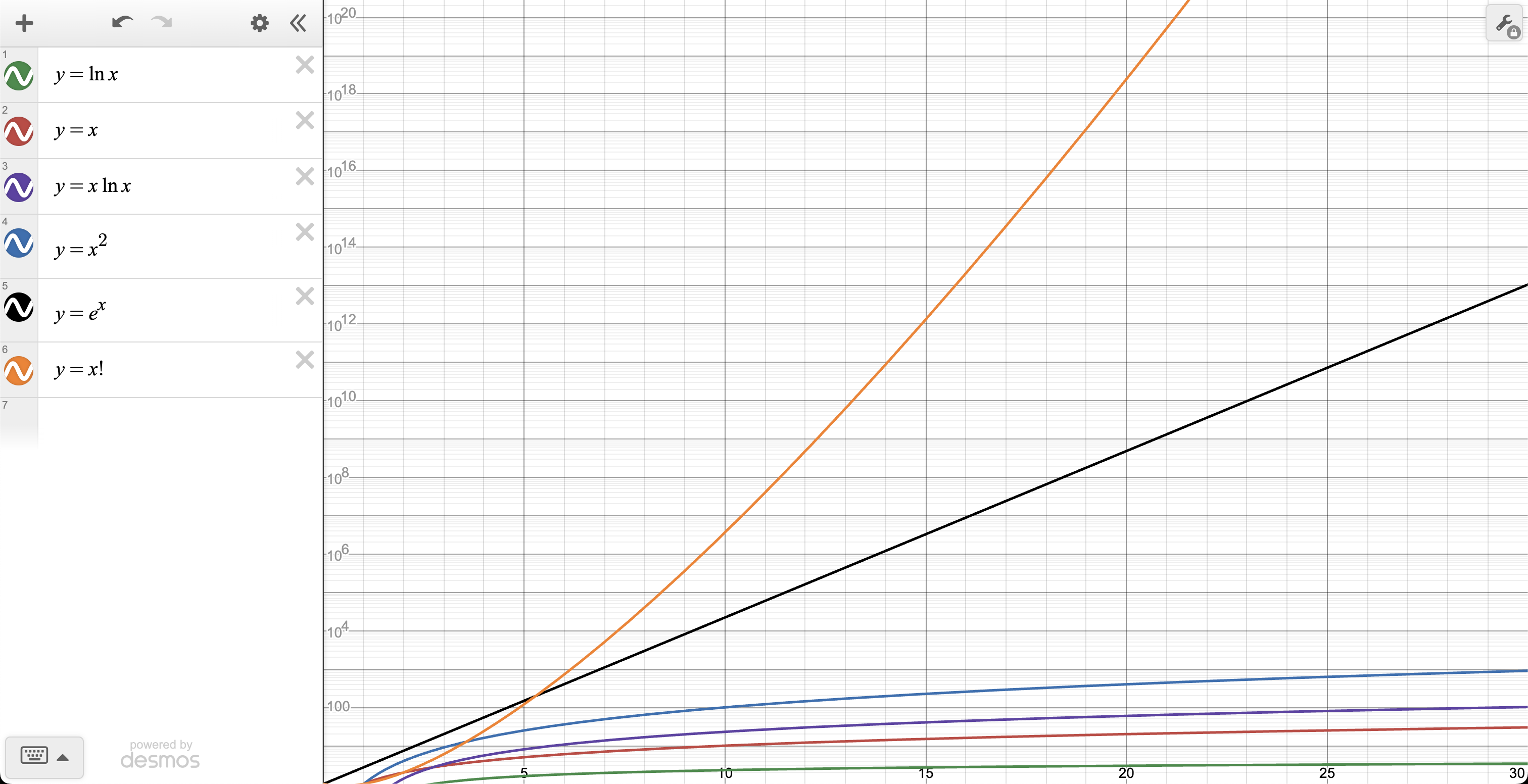
So sánh tốc độ tăng trưởng

Khái niệm tốc độ tăng trưởng có thể đo lường thông qua đạo hàm. Một cách trực giác, ta có thể hiểu rằng, khi tốc độ tăng trưởng của 2 hàm là khác nhau, hàm tăng trưởng nhanh hơn sẽ ngày càng “bỏ xa” hàm tăng trưởng chậm hơn. Điều này có thể được thấy rõ qua việc tính giới hạn của tỉ số giữa 2 hàm khi $x \to +\infty$.

$$ \lim_{x \to +\infty} \frac{f(x)}{g(x)} = \begin{cases} 0 & \text{nếu } f(x) \text{ tăng chậm hơn } g(x) \\ \infty & \text{nếu } f(x) \text{ tăng nhanh hơn } g(x) \\ \text{hằng số} & \text{nếu } f(x) \text{ và } g(x) \text{ tăng cùng tốc độ} \end{cases} $$

Áp dụng cho các hàm đã giới thiệu ở trên:

$$ \begin{align*} &\lim_{x \to +\infty} \dfrac{\ln x}{x} \overset{L'hôpital}{=} \lim_{x \to +\infty} \dfrac{1/x}{1} = 0 \\ &\lim_{x \to +\infty} \dfrac{x}{x \ln x} = \lim_{x \to +\infty} \dfrac{1}{\ln x} = 0 \\ &\lim_{x \to +\infty} \dfrac{x \ln(x)}{x^2} = \lim_{x \to +\infty} \dfrac{\ln(x)}{x} = 0 \\ &\lim_{x \to +\infty} \dfrac{x^2}{e^x} \overset{L'hôpital}{=} \lim_{x \to +\infty} \dfrac{2x}{e^x} \overset{L'hôpital}{=} \lim_{x \to +\infty} \dfrac{2}{e^x} = 0 \end{align*} $$

Đến đây vẫn còn thiếu hàm giai thừa. Thường thì ta chỉ dùng hàm giai thừa với $x\in\mathbb{N}$. Tổng quát hoá cho $x\in\mathbb{R}, x>0$ ta được:

$$x! = \Gamma(x+1) = \int_0^{+\infty} t^x e^{-t} dt$$

với $\Gamma$ là hàm gamma. Tuy nhiên, hàm gamma không thể tính giới hạn với hàm khác một cách dễ dàng như các hàm trên. Tôi sẽ quay lại với nó trong một bài viết khác. Ta sẽ tạm chấp nhận rằng:

$$\lim_{x \to +\infty} \dfrac{e^x}{x!} = 0$$

Kết luận

Tốc độ tăng trưởng của các hàm giải tích là công cụ mạnh mẽ giúp ta nhanh chóng có cái nhìn trực giác về hành vi của chúng trên đoạn $[0, +\infty)$, từ đó có cơ sở cho các ý tưởng chứng minh.

Nhìn chung, Hàm có liên quan logarit có tốc độ tăng trưởng tương đối chậm, trong khi các hàm như $e^x$ và $n!$ vượt trội hơn hẳn. Sự xuất hiện của các hàm này (ở mẫu số) thường là chỉ báo cho sự hội tụ nhanh chóng của dãy hay chuỗi tương ứng.