NZQIRC
Posts Tags Categories Docs About
NZQIRC

Nội dung

Lí thuyết phạm trù, thật ra là cái gì vậy?

 trong Category-Theory
   2380 từ   12 phút 

Thay vì đưa ra một loạt định nghĩa — khá dễ kiếm trên internet nhưng bạn có thể sẽ cảm thấy hơi khó hiểu khi mới tiếp xúc — tôi nghĩ sẽ thú vị hơn nếu chúng ta cùng nhìn nhận lí thuyết phạm trù (category theory) trong bức tranh lớn hơn của toán học. Lí thuyết này khác biệt so với các nhánh toán học khác. Thay vì là một lĩnh vực ngang hàng với các ngành khác, nó giống như một “gen chung” kết nối chúng lại ngay từ gốc rễ.

Bức tranh toàn cảnh của toán học

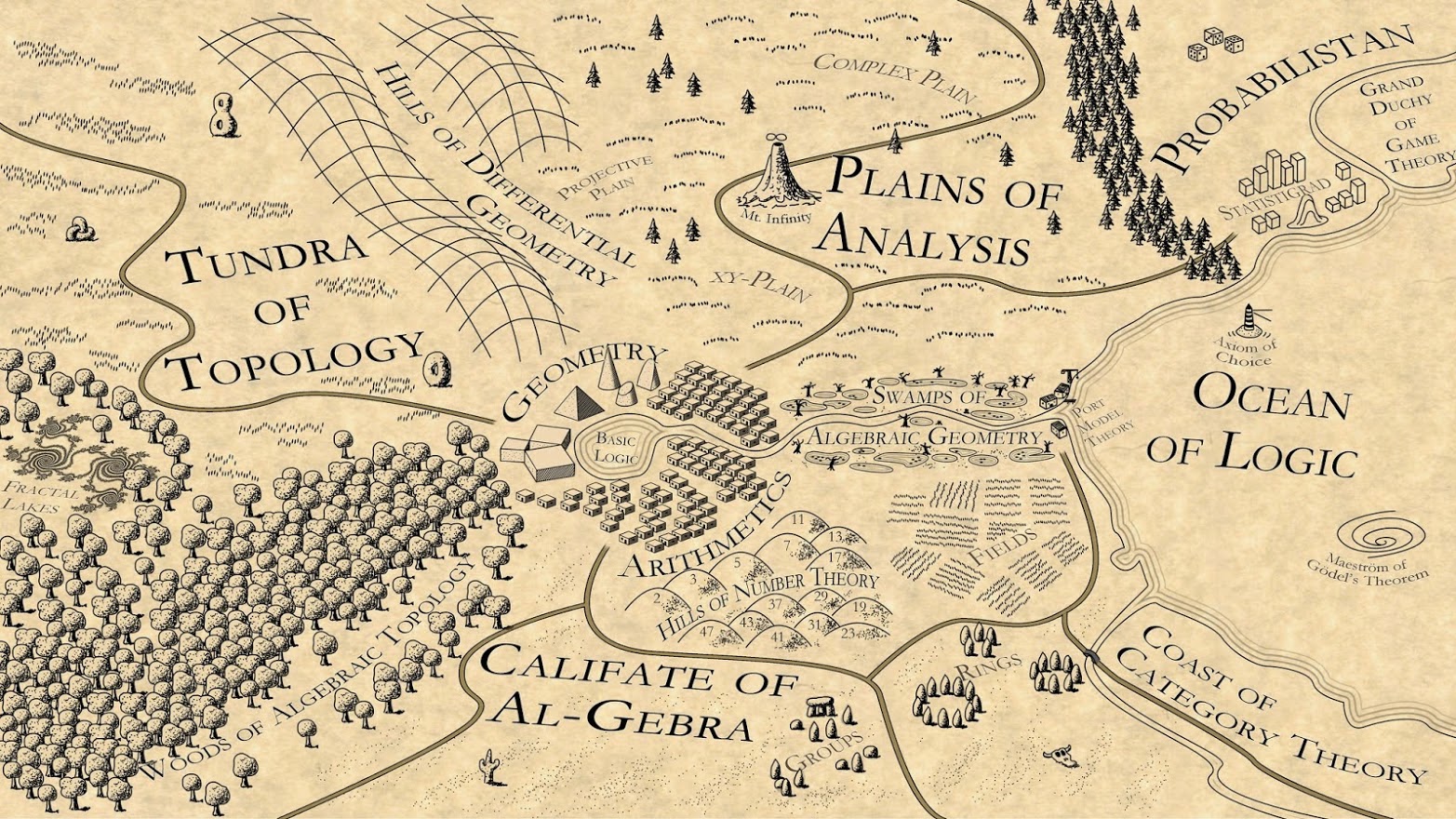
Martin Kuppe từng tạo ra một bản đồ tuyệt vời về các “cảnh quan toán học” mà anh ấy gọi là “Mathematistan” (Miền đất toán học). Bạn sẽ thấy rằng “bờ biển của lí thuyết phạm trù” nằm ở góc dưới bên phải. Theo quan điểm của tôi, lí thuyết phạm trù không hẳn là một vùng đất nào đó trên bản đồ, mà là một cách để có được cái nhìn từ trên cao về toàn cảnh. Nó giống như việc nâng đôi chân của chúng ta lên khỏi mặt đất và mang lại cho chúng ta một góc nhìn toàn diện từ trên không.

Từ vị trí này, bạn sẽ nhận ra rằng các lĩnh vực (realm) khác nhau của toán học lại có những mô thức (pattern)/xu hướng (trend) và cấu trúc (structure) chung. Điều này trở nên vô cùng hữu ích khi bạn muốn giải quyết một vấn đề trong lĩnh vực nào đó (chẳng hạn như Topo) nhưng không có đủ công cụ phù hợp. Bằng cách chuyển vấn đề sang một lĩnh vực khác (chẳng hạn như đại số), bạn có thể nhìn vấn đề từ một góc độ mới và có thể tìm ra những công cụ mới, từ đó giải pháp sẽ trở nên dễ dàng hơn.

Lí thuyết phạm trù cũng chỉ ra những chiếc cầu nối giữa các lĩnh vực này. Nó chỉ rõ những cấu trúc chung của các lĩnh vực: mỗi lĩnh vực đều có các đối tượng (lí thuyết phạm trù gọi đối tượng là “vật”, trong tiếng Anh thì đều cùng một từ “object”) trong đó (lí thuyết tập hợp có các tập hợp (set), lí thuyết nhóm có các nhóm (group), Topo có các không gian topo (toplogical space),…) và những đối tượng (vật) này có thể liên quan với nhau (các tập hợp liên kết thông qua hàm số (function), các nhóm liên kết qua đồng cấu (homomorphisms), các không gian topo liên kết qua các hàm liên tục (continuous functions),…) theo những cách hợp lí (phép hợp thành (composition) và tính kết hợp (associativity)).

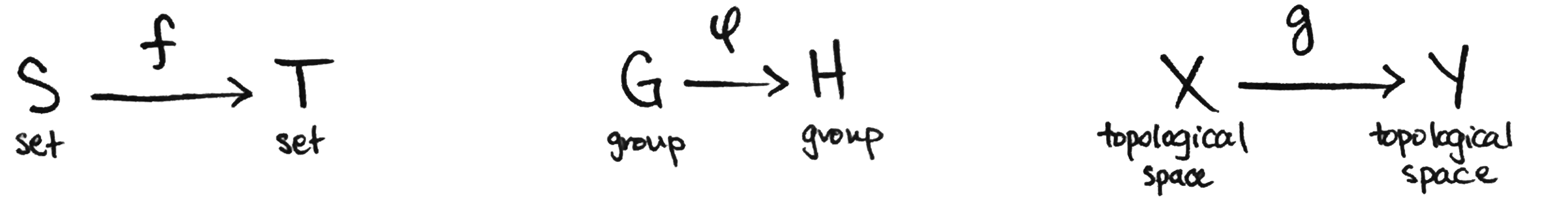
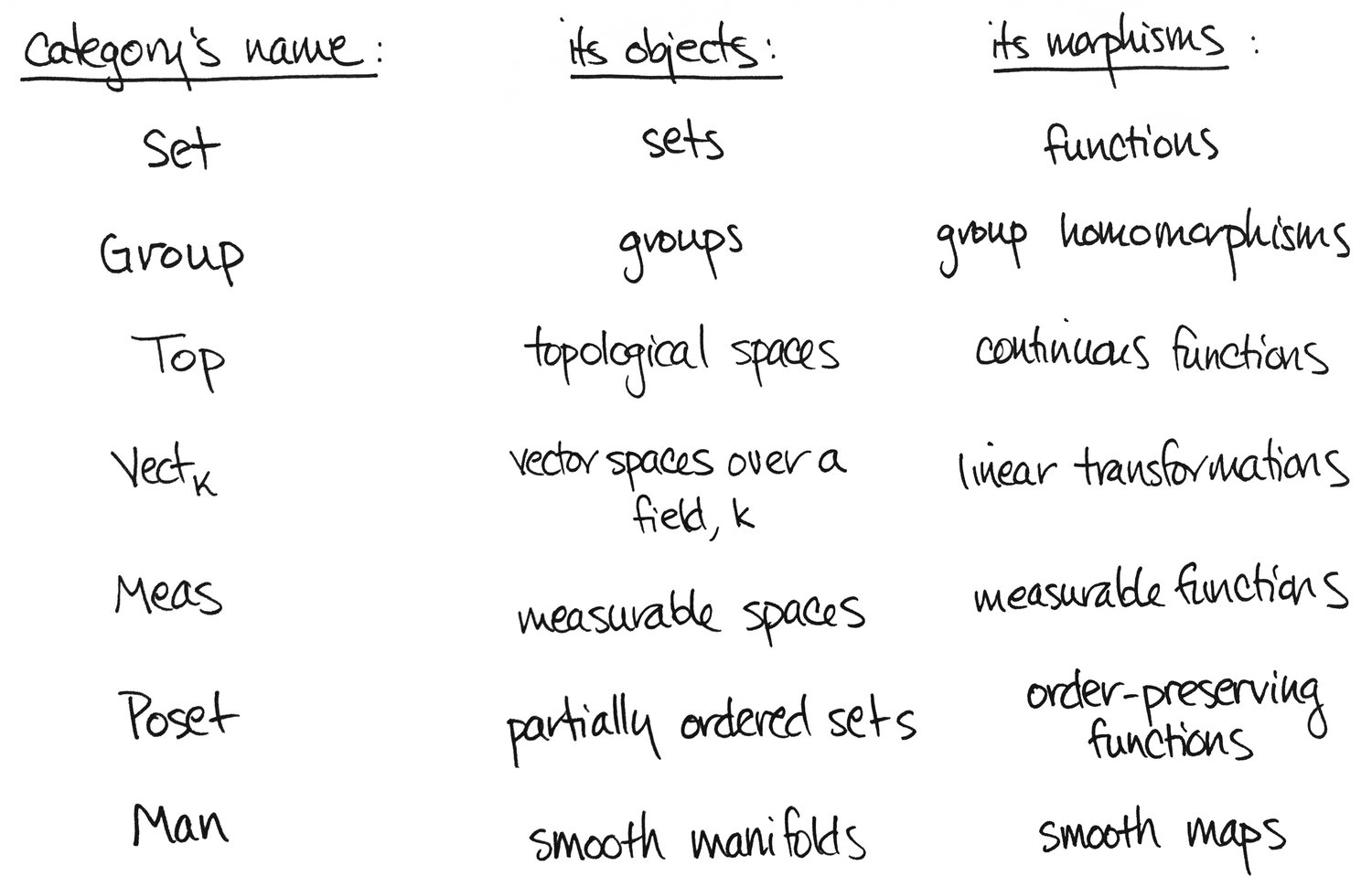
Một phạm trù (category), về cơ bản, là bộ (collection) nào đó gồm các đối tượng (vật) có thể liên kết (relate) với nhau qua các cấu xạ (morphisms) theo những cách hợp lí (sensible ways), như phép hợp thành (composition) và tính kết hợp (associativity). Như Barry Mazur từng nhận xét, đây là một “khuôn mẫu” (template) cho toàn bộ toán học: tuỳ thuộc vào những gì bạn đưa vào khuôn mẫu đó, bạn sẽ thu được một trong những lĩnh vực toán học. Ví dụ, tập hợp các tập hợp (sets) với các hàm số (functions) tạo thành một phạm trù, cũng như tập hợp các nhóm (groups) với các đồng cấu nhóm (group homomorphisms), và các không gian topo với các hàm liên tục. Ngoài những ví dụ này, đây là một số phạm trù khác mà có lẽ bạn cũng đã quen thuộc:

Vấn đề rốt cuộc nằm ở các “quan hệ”!

Một trong những đặc điểm nổi bật của lí thuyết phạm trù là nó loại bỏ nhiều chi tiết phức tạp: nó không quan tâm đến các phần tử (element) cụ thể trong tập hợp (set) của bạn, cũng chẳng quan trọng nhóm của bạn có giải được hay không, hay không gian topo của bạn có cơ sở đếm được hay không. Vậy nên, cũng khá tự nhiên nếu bạn này ra thắc mắc rằng? Ủa vậy thì nó hữu ích chỗ nào?

Các đối tượng toán học được xác định (determined) và được hiểu (understood) thông qua mạng lưới mối quan hệ của chúng với tất cả các đối tượng khác cùng loại.

Barry Mazur

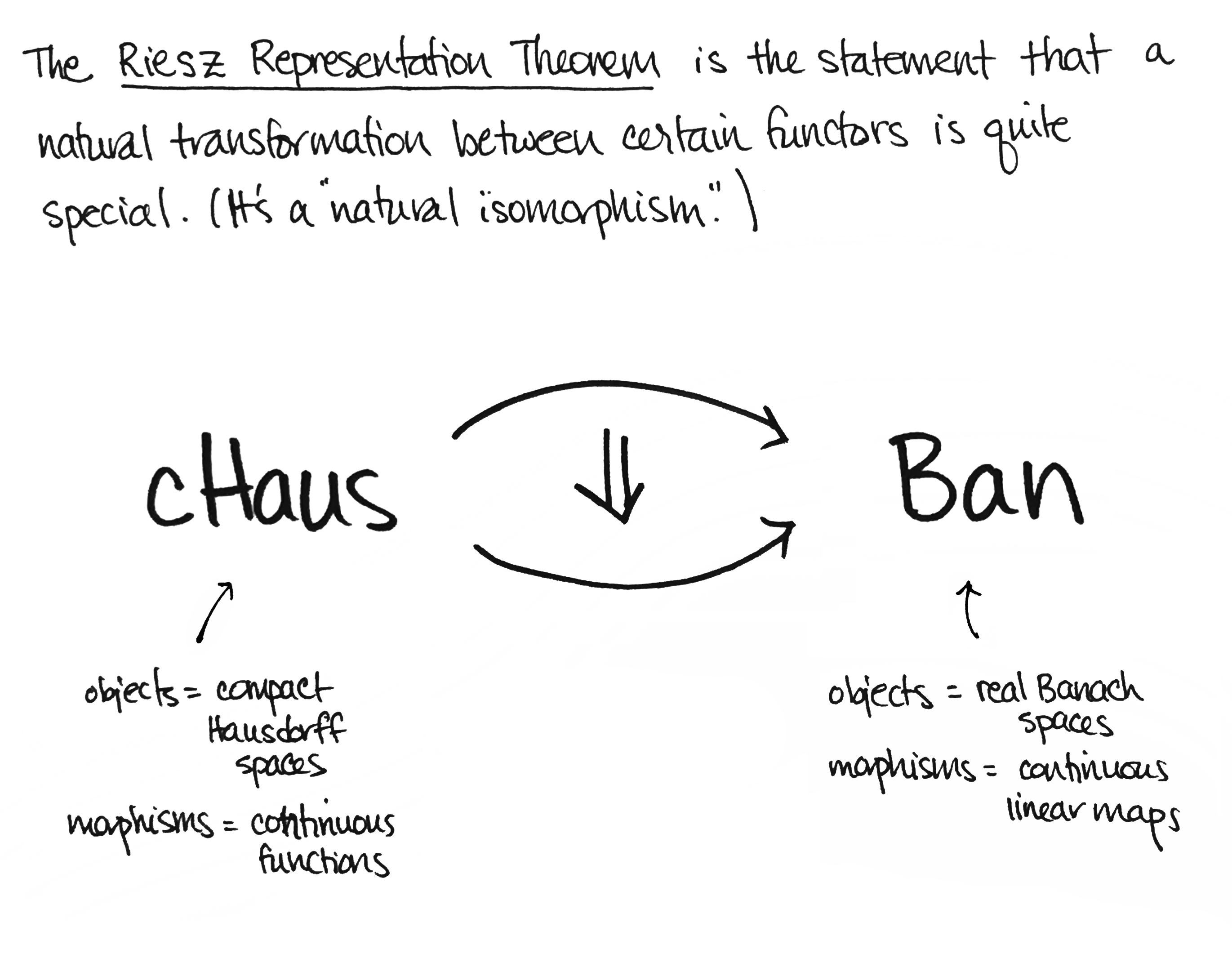
Ưu điểm của việc không chú trọng vào chi tiết là nó hướng sự chú ý của bạn từ các đối tượng (vật) cụ thể sang các mối quan hệ giữa các đối tượng (vật) đó (tức là các cấu xạ - morphisms). Một cách tự nhiên, bạn sẽ đặt câu hỏi về các mối quan hệ giữa các phạm trù. Chúng được gọi là các hàm tử (functor). Tiếp tục, vậy, còn mối quan hệ giữa các mối quan hệ thì sao? Đó là các phép biến đổi tự nhiên (natural transformations). (Và đúng vậy, bạn có thể hỏi một chuỗi câu hỏi như: “Còn mối quan hệ giữa mối quan hệ của các mối quan hệ thì sao?” Điều này dẫn đến phạm trù vô hạn - infinity categories. [Và có thể khiến bạn “đứng hình”.] Để biết thêm chi tiết, xem tại đây.) Nghe có vẻ như điều gì đó xa vời, nhưng những ý tưởng này - phạm trù, hàm tử, và các phép biến đổi tự nhiên - dẫn đến một kho tàng lí thuyết xuất hiện ở hầu hết mọi nơi.

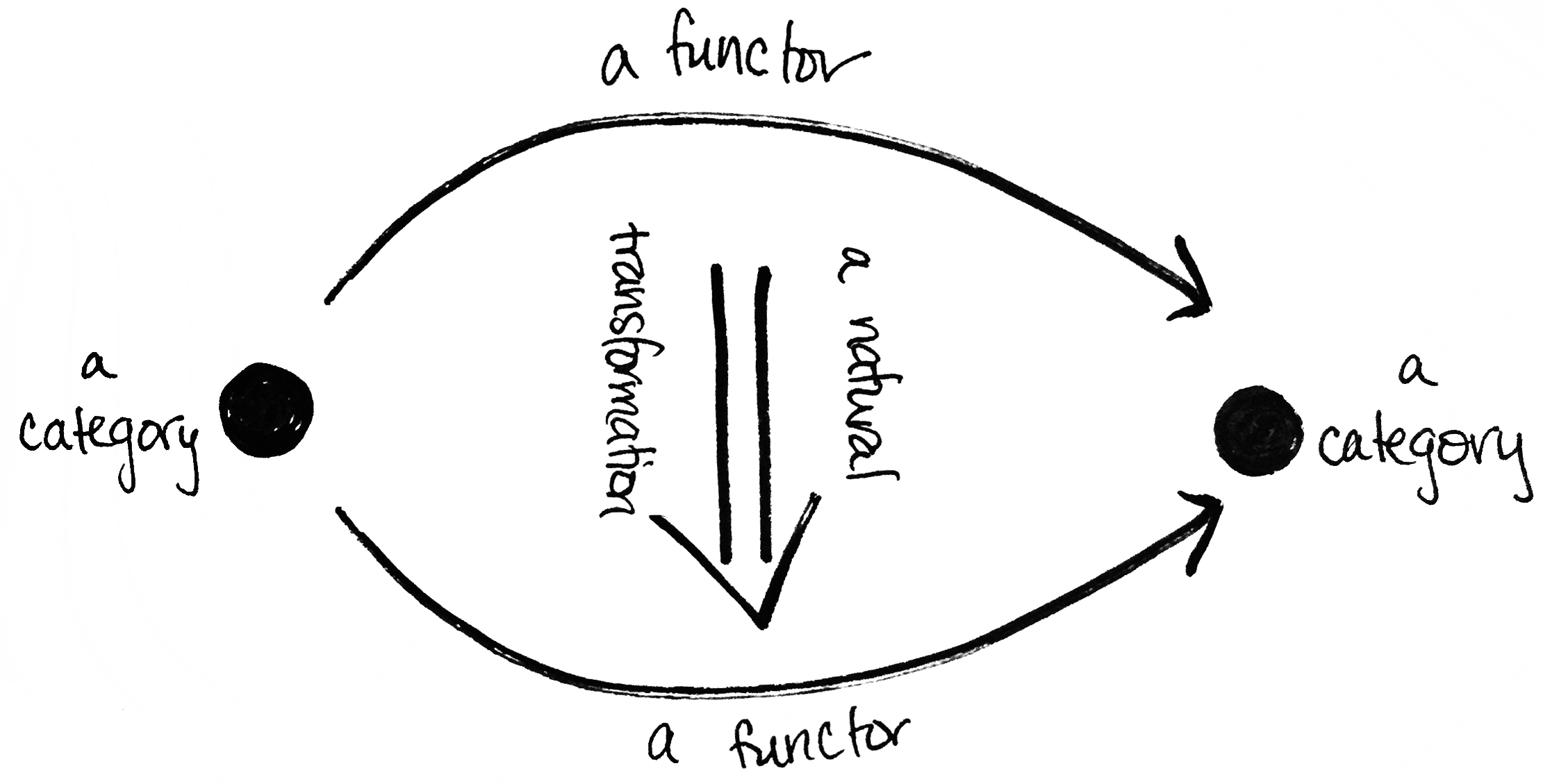
Dưới đây là một số bằng chứng, hầu hết tôi đã lấy từ cuốn sách xuất sắc Category Theory in Context của Emily Riehl.

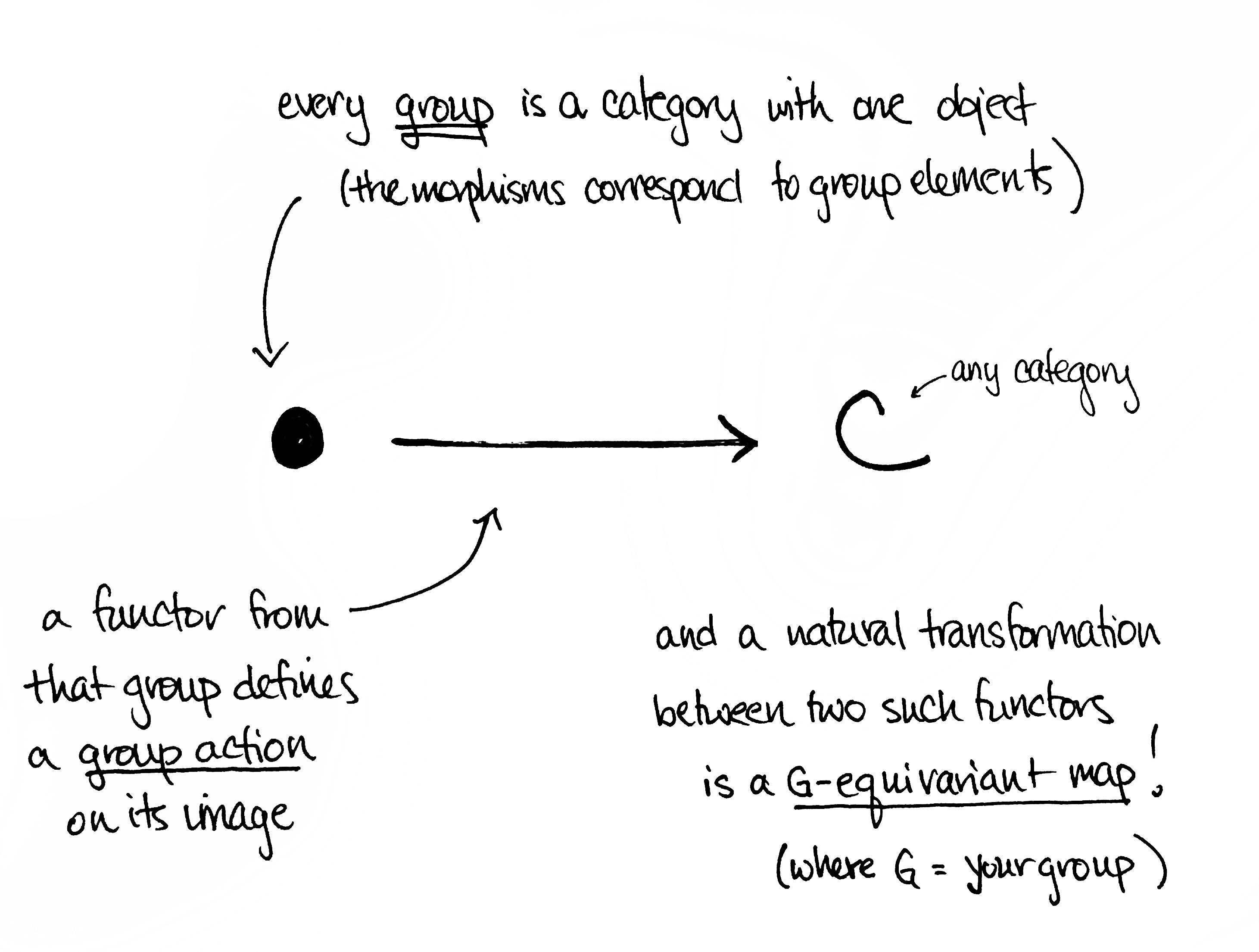
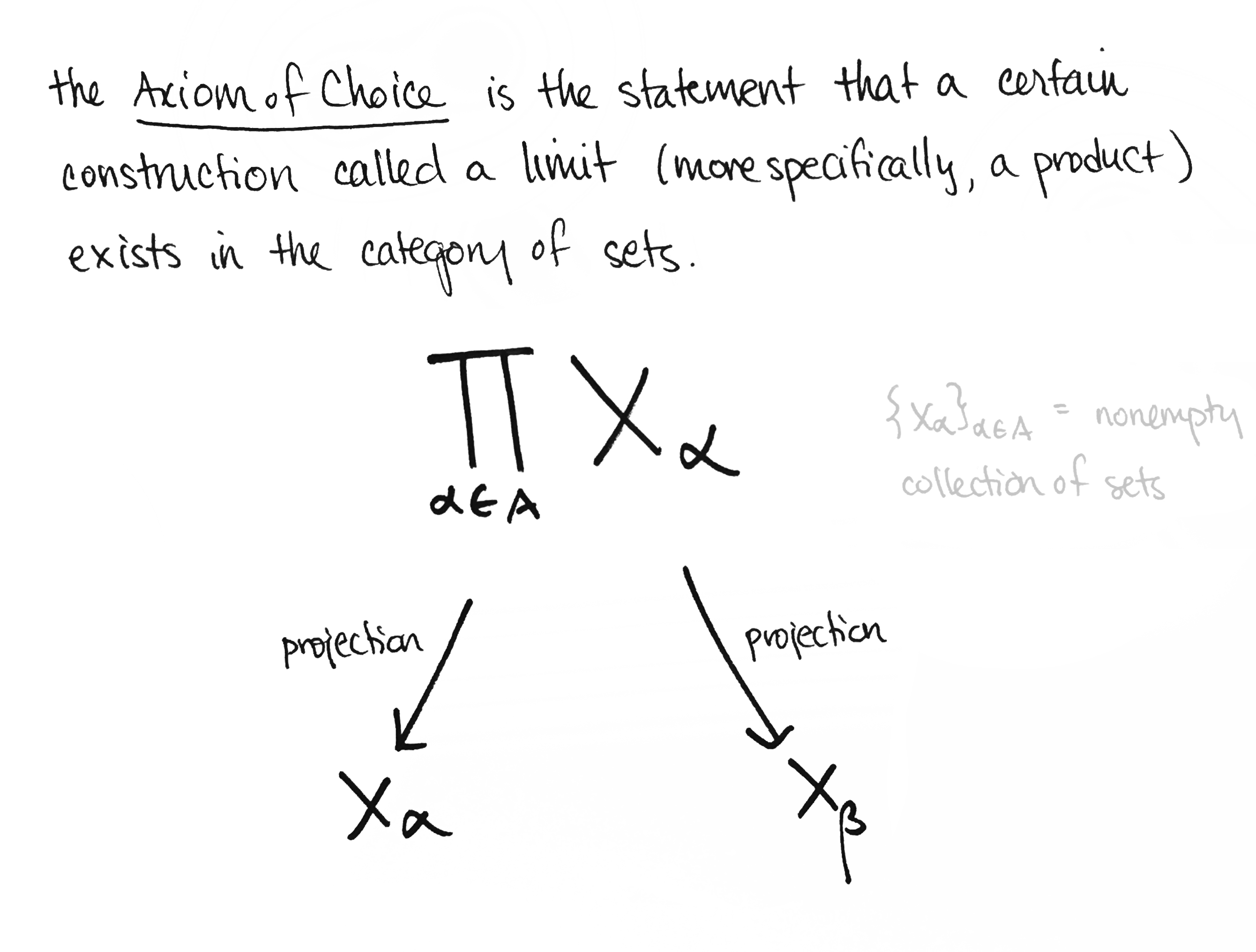
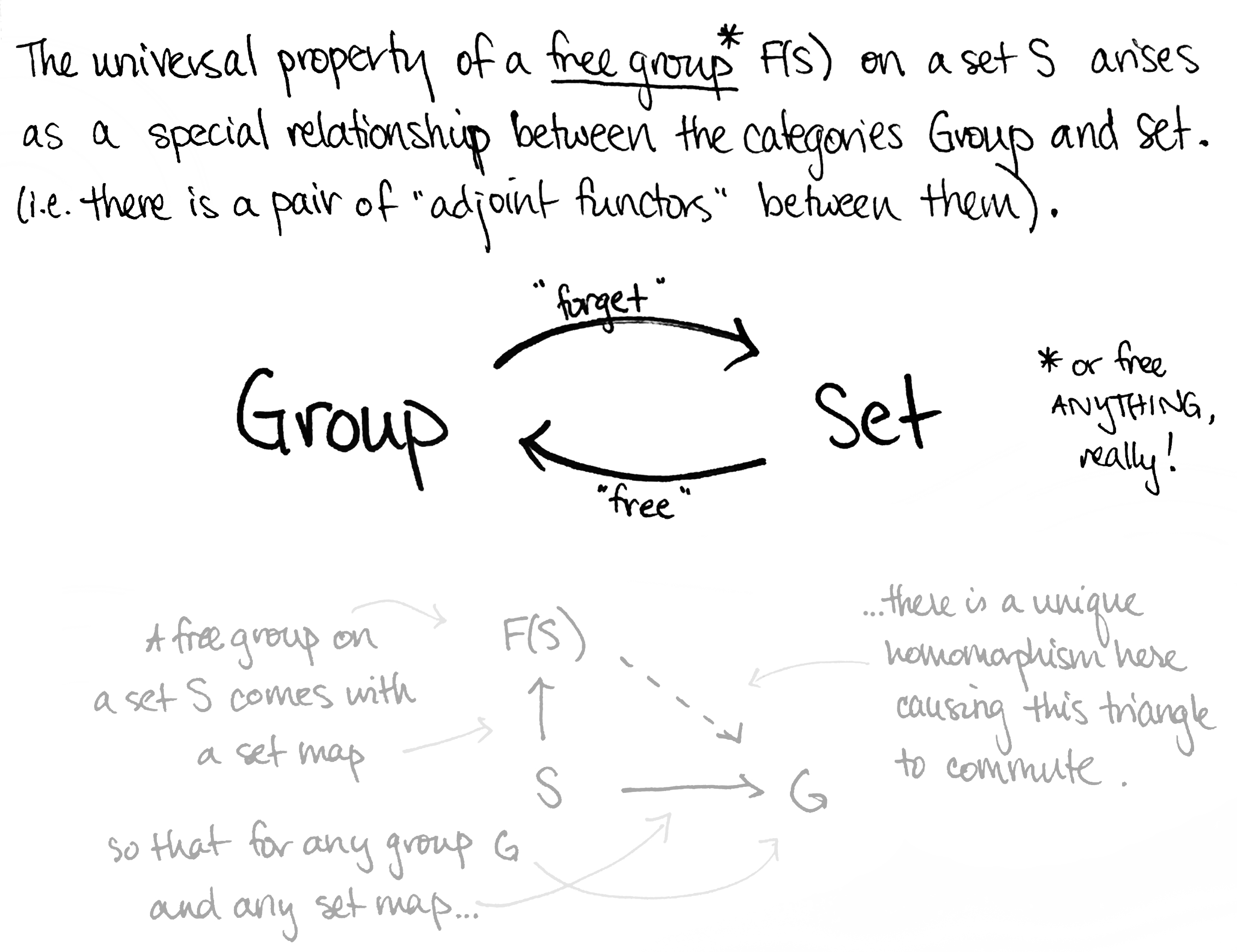
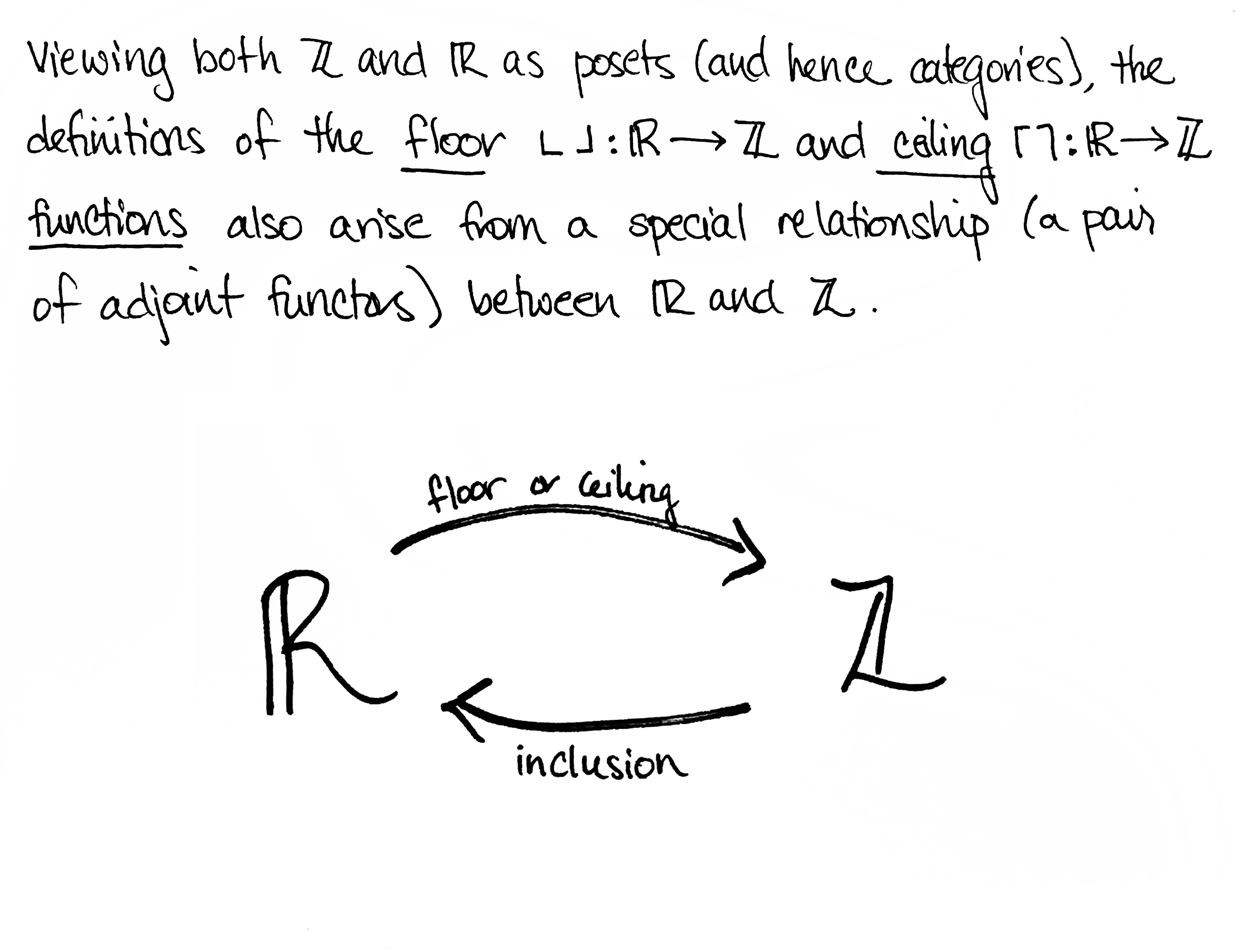
Nhưng, tại sao lại là lí thuyết phạm trù?

Tôi nhận ra rằng các “phạm trù” có thể giống như “cá cơm”: một số người thích, một số người không, và một số người cần thời gian để dần dần quen thuộc với chúng. Thật vậy, lí thuyết phạm trù có thể không giúp bạn tìm delta cho epsilon của mình, hay xác định xem nhóm có cấp 520 của bạn có đơn giản hay không, hoặc tìm ra giải pháp cho phương trình vi phân của bạn. Để thực hiện những nhiệm vụ đó, chúng ta phải đặt chân xuống đất. Nhưng suy nghĩ theo hướng lí thuyết phạm trù có thể giống như một ngọn hải đăng — giúp tăng cường trực giác và làm sắc nét sự hiểu biết của bạn khi bạn khám phá những ngóc ngách trong các lĩnh vực toán học yêu thích của mình. (Như Freeman Dyson từng nói, chúng ta cần cả những chú chim và những chú ếch để thúc đẩy tiến bộ toán học!)

Tôi cũng nghĩ rằng sức hấp dẫn của lí thuyết phạm trù phụ thuộc rất nhiều vào mục tiêu của bạn với tư cách là một nhà toán học. Lí thuyết này rất thu hút tôi vì tôi yêu việc khám phá các kết nối giữa những thứ tưởng chừng như không liên quan. Thực tế, đó chính là điều đã đưa tôi đến với toán học ngay từ đầu — không phải vì một vấn đề cụ thể trong hình học, giải tích hay đại số, mà bởi ý tưởng rằng có những kết nối tiềm ẩn giữa chúng chỉ chờ được khám phá.

Tóm lại, sự phổ biến của lí thuyết phạm trù trong toán học đã trở nên khá rõ ràng. Vậy nên, dù mục tiêu toán học của bạn là gì, tôi nghĩ việc học một chút về lí thuyết phạm trù chắc chắn sẽ rất đáng giá! Dưới đây là một vài tài liệu hay để bạn bắt đầu:

  • Basic Category Theory của Tom Leinster có thể tiếp cận ở trình độ đại học (câu đầu tiên của cuốn sách là “Đây không phải là một cuốn sách chuyên sâu.”) và chắc chắn là dễ hiểu ở trình độ sau đại học. Tôi cũng thích cuốn sách của Emily Riehl mà tôi đã nhắc đến trước đó. Một phiên bản PDF miễn phí có sẵn trên trang web của cô ấy.
  • Cuốn sách kinh điển là Categories for the Working Mathematician của Saunders Mac Lane, người đã phát triển lí thuyết phạm trù cùng với Samuel Eilenberg vào những năm 1940.
  • Đây là một bài viết của John D. Cook, trong đó ông nói về tích (Cartesian) từ quan điểm của phạm trù — lưu ý rằng có sự nhấn mạnh vào các mối quan hệ!
  • Khi bạn đã nắm được các định nghĩa cơ bản, đây là một số video YouTube (bao gồm cả một số của Eugenia Cheng) về các chủ đề lí thuyết phạm trù nâng cao hơn.

Trong các bài viết tới, tôi sẽ đi qua các định nghĩa chính xác của một phạm trù, một hàm tử và một biến đổi tự nhiên cùng với một số ví dụ.

“Lí thuyết tổng quát tốt không tìm kiếm sự tổng quát tối đa (masimum generality), mà tìm kiếm sự tổng quát phù hợp (right generality).”

Saunders Mac Lane

Ngôn ngữ của lí thuyết phạm trù:

Học lí thuyết phạm trù cũng tương tự như học một ngoại ngữ ngôn ngữ nào đó vậy. Bằng cách nắm vững các “từ vựng” và “ngữ pháp” cơ bản, ta có thể có có cách tiếp cận dễ hiểu hơn.

Trong cách nhìn của tôi, vai trò của lí thuyết phạm trù đối với toán học như một lưu đồ (flowchart). Nó là hệ thống kí hiệu để giúp ta thấy ra các mối quan hệ toán học phức tạp. Nếu lưu đồ giúp trực quan hoá các quy trình và các bước ra quyết định, thì lí thuyết phạm trù cho ta một khung sườn để trực quan hoá, sơ đồ hoá các khái niệm toán học và mối quan hệ của chúng một cách hệ thống. Trong đó

  • Lưu đồ: Bắt đầu từ một điểm, có các mũi tên chỉ quy trình hoặc quyết định và dẫn đến các kết quả khác nhau dựa trên đầu vào và điều kiện.

  • Phạm trù: Bao gồm các vật (tương tự như các ô trong lưu đồ) và các cấu xạ (morphisms) (tương tự như các mũi tên) đại diện cho các mối quan hệ hoặc ánh xạ (map) giữa các đối tượng này.

Cả hai đều là công cụ để tổ chức thông tin, nhưng lí thuyết phạm trù hoạt động ở một cấp độ trừu tượng và tổng quát hơn.

Các thành phần cơ bản của lí thuyết phạm trù

  • Các vật: Đại diện cho các thực thể trong phạm trù. Trong phạm trù Set, chẳng hạn, các vật là các tập hợp.

  • Các cấu xạ: Đại diện cho các mối quan hệ hoặc hàm giữa các vật. Trong Set, các cấu xạ là các hàm giữa các tập hợp.

Ta có thể hình dung phạm trù có thể được hình dung như một đồ thị với các vật là các nút và các cấu xạ là các cạnh có hướng nối các nút này. Tuy nhiên, khác với các đồ thị thông thường, các phạm trù bao gồm cấu trúc bổ sung thông qua phép hợp thành (composition) của các cấu xạ và sự tồn tại của các ánh xạ đồng nhất (identity morphisms).

  • Phép hợp các cấu xạ: Cho phép nối các cấu xạ để tạo thành các cấu xạ mới, tuân theo các quy tắc cụ thể.

  • Cấu xạ Đồng nhất: Mỗi vật có một cấu xạ đồng nhất đóng vai trò là yếu tố trung lập (neutral element) cho phép hợp thành.

  • Tính Kết hợp: Phép hợp các cấu xạ có tính kết hợp, nghĩa là thứ tự thực hiện các phép hợp thành không ảnh hưởng đến kết quả.

Các tiên đề này đảm bảo rằng phạm trù duy trì cấu trúc nhất quán và dễ quản lí, giúp dễ dàng xử lí các mối quan hệ phức tạp về mặt toán học.

Lí thuyết phạm trù là sự tổng quát hóa của khái niệm lưu đồ. Nó không chỉ tổ chức các mối quan hệ giữa các vật (giống như lưu đồ tổ chức các quy trình) mà còn bổ sung các phép toán như phép hợp thành, cho phép xử lí các mối quan hệ này theo cách phức tạp và trừu tượng hơn. Sự tổng quát hóa này cho phép lí thuyết phạm trù xử lí hiệu quả cả cấu trúc hữu hạn và vô hạn.

Sự phân cấp của các cấu xạ

Đây là một trong những trọng tâm trong lí thuyết phạm trù. Cụ thể, các cấu xạ có thể được phân cấp dựa trên mức độ quan trọng và sự phức tạp của chúng:

  • Cấu xạ (quan hệ giữa các vật): Quan trọng hơn bản thân các vật.
  • Quan hệ giữa các cấu xạ (quan hệ giữa các quan hệ giữa các vật): Thậm chí còn quan trọng hơn, dẫn đến các khái niệm như biến đổi tự nhiên (natural transformation).
  • Quan hệ bậc cao (quan hệ giữa… các quan hệ giữa các quan hệ giữa các vật): Lí thuyết có thể mở rộng đến các quan hệ giữa các quan hệ của ánh xạ, cho thấy mức độ sâu sắc và tính đa tầng của lí thuyết phạm trù.

Tham khảo

Cập nhật ngày 2024-Oct-21
Đọc với định dạng Markdown
Quay lại | Trang chủ