Định lí hàm ẩn - Implicit Function Theorem
Các bài toán tối ưu có ràng buộc (Lagrange), ổn định trong hệ động lực (stability in dynamical systems), hình học (geometry), topo (topology), kinh tế (comparative statics), học máy (machine learning), robot (robotics - Kinematics), thuỷ động lực học (Fluid Dynamics) … thường dẫn đến các phương trình nhiều biến kiểu như:
$$ F(x_0, x_1, x_2, \dots, x_n) = 0. $$Đôi khi việc tìm nghiệm của phương trình trên là không thể, tốn nhiều tài nguyện hoặc thậm chí là không cần thiết. Thay vào đó, một nhu cầu khác thường phát sinh, đó là lúc ta nghi ngờ rằng có sự phụ thuộc ngầm giữa các biến (có thể chỉ tồn tại trong một phạm vi cục bộ nào đó) và ta muốn xác định điều kiện để biểu diễn một (hoặc một vài biến) biến dưới dạng hàm của các biến còn lại. Nội dung của Định lí hàm ẩn (Implicit Function Theorem) chính là để giải quyết vấn đề này.
1. Phát biểu (trường hợp 2 biến thực)
Giả sử:
- $F(x, y)$ là một hàm khả vi liên tục (continuously differentiable function) trong lân cận của điểm $(x_0, y_0)$,
- $F(x_0, y_0) = 0$,
- $\dfrac{\partial F}{\partial y}(x_0, y_0) \neq 0$,
khi đó tồn tại một lân cận của $x_0$ trong đó:
- tồn tại một hàm $y = g(x)$ khả vi liên tục, và
- $F(x, g(x)) = 0$ với mọi $x$ trong lân cận đó.
2. Hình dung hình học
$$F(x, y) = x^2 + y^2 - 1 = 0\qquad (1)$$mô tả một đường tròn bán kính $1$ trong $\mathbb{R}^2$.
Ý tưởng chính - độ phẳng cục bộ
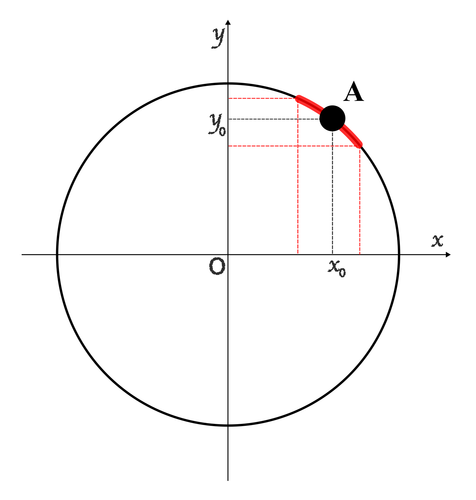
cho thấy đoạn-kha-khá-thẳng này có độ “nghiêng” nhất định , và do đó cho phép ta coi $y$ là một hàm của $x$ xét trong lân cận tương ứng quanh $x_0$ (giờ bạn hiểu vì sao lại gọi nó là hàm ẩn rồi đấy).
Tiếp theo - xấp xỉ bằng khai triển Taylor
$$ F(x, y) \approx F(x_0, y_0) + \dfrac{\partial F}{\partial x}(x_0, y_0)(x - x_0) + \dfrac{\partial F}{\partial y}(x_0, y_0)(y - y_0). $$Nếu $\dfrac{\partial F}{\partial y}(x_0, y_0) \neq 0$, thì thành phần chứa $(y - y_0)$ đóng vai trò chính, cho phép ta giải $y$ theo $x$.
Tóm lại
Trực giác của định lý hàm ẩn trong $\mathbb{R}^2$ là: Nếu đường cong $F(x, y) = 0$
- đủ mượt mà, tức là $F(x,y)$ khả vi liên tục, và
- có độ nghiêng nhất định tại lân cận của một điểm $(x_0, y_0)$, tức là $$\dfrac{\partial F}{\partial y}(x_0, y_0)\neq 0,$$
thì ta có thể xem $y$ là một hàm của $x$ trong lân cận của $x_0$.
3. Mở rộng cho trường hợp nhiều biến hơn
$$ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \in \mathbb{R}^n, \qquad \mathbf{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix} \in \mathbb{R}^m. $$Để dễ liên tưởng, tôi tổng hợp lại trong bảng sau:
| Điểm chung | Trường hợp 2 biến | Trường hợp nhiều biến hơn |
|---|---|---|
| Biến $x$ | $x \in \mathbb{R}$ | $\mathbf{x} \in \mathbb{R}^n$ |
| Biến $y$ | $y \in \mathbb{R}$ | $\mathbf{y} \in \mathbb{R}^m$ |
| Hàm $F$ | $F: \mathbb{R}^2 \to \mathbb{R}$ | $F: \mathbb{R}^n \to \mathbb{R}^m$ |
| Điểm $(x_0, y_0)$ | $(x_0, y_0) \in \mathbb{R}^2$ | $(\mathbf{x}_0, \mathbf{y}_0) \in \mathbb{R}^{n+m}$ |
| Tính trơn | $F(x, y)$ khả vi liên tục trong lân cận của $(x_0, y_0)$ | $F(\mathbf{x}, \mathbf{y})$ khả vi liên tục trong lân cận của $(\mathbf{x}_0, \mathbf{y}_0)$ |
| Tính nghiêng | $\dfrac{\partial F}{\partial y}(x_0, y_0) \neq 0$ | ${\color{orange}\det}\left(\dfrac{\partial F}{\partial \mathbf{y}}(\mathbf{x}_0, \mathbf{y}_0)\right) \neq 0$ |
| Hàm ẩn | $y = g(x)$ khả vi liên tục và $F(x, g(x)) = 0$ | $\mathbf{y} = \mathbf{g}(\mathbf{x})$ khả vi liên tục và $F(\mathbf{x}, \mathbf{g}(\mathbf{x})) = 0$ |
| Đạo hàm hàm ẩn | $\dfrac{\partial g}{\partial x} = -\dfrac{\dfrac{\partial F}{\partial x}(x, g(x))}{\dfrac{\partial F}{\partial y}(x, g(x))}$ | $\dfrac{\partial \mathbf{g}}{\partial \mathbf{x}} = -\left(\dfrac{\partial F}{\partial \mathbf{x}}\right)^{-1}\dfrac{\partial F}{\partial \mathbf{y}}$ |
Và trực giác cho trường hợp mở rộng này cũng tương tự như trường hợp 2 biến. Đó là: Nếu mặt cong $F(\mathbf{x}, \mathbf{y}) = 0$
- đủ mượt mà, tức là $F(\mathbf{x}, \mathbf{y})$ khả vi liên tục, và
- có độ nghiêng nhất định tại lân cận quanh điểm $(\mathbf{x}_0, \mathbf{y}_0)$, tức là $$\det\left(\dfrac{\partial F}{\partial \mathbf{y}}(\mathbf{x}_0, \mathbf{y}_0)\right)\neq 0,$$
thì ta có thể xem $\mathbf{y}$ là một hàm của $\mathbf{x}$ trong lân cận của $\mathbf{x}_0$.
4. Tiếp tục mở rộng
Điểm tổng quát hoá đáng kể nhất nằm ở ma trận Jacobi $\dfrac{\partial F}{\partial \mathbf{y}}$ thay cho đạo hàm riêng $\dfrac{\partial F}{\partial y}$ trong trường hợp 2 biến thực. Bạn có biết vì sao ma trận Jacobi lại xuất hiện ở đây không? và nó có ý nghĩa tương tự với đạo hàm riêng trong trường hợp 2 biến thực thế nào?