Diện tích hình bình hành tạo bởi 2 vector

Ý tưởng

Diện tích hình bình hành tạo bởi 2 vector

$$u = \begin{bmatrix} a \\ c \end{bmatrix},\qquad v = \begin{bmatrix} b \\ d \end{bmatrix}$$

được minh họa như sau:

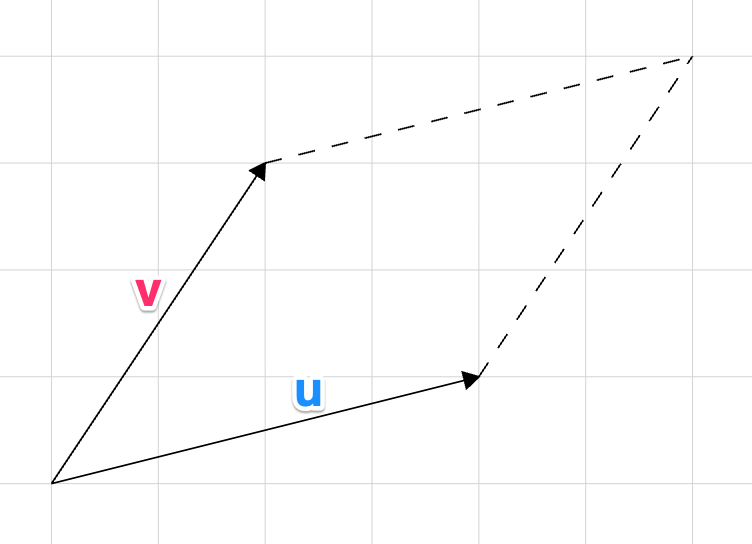
Để tính phần diện tích hình bình hành, ta sẽ lấy phần diện tích của hình chữ nhật ngoài cùng trừ cho phần diện tích của 4 tam giác nhỏ (đánh số 1,2,3,4) và 2 hình chữ nhật nhỏ ở 2 góc (đánh số 5, 6). Bằng kiến thức hình học sơ cấp, ta có thể nhanh chóng nhẩm ra kích thước các cạnh của tất cả tam giác và hình chữ nhật đó dựa trên toạ độ của 2 vector $u$ và $v$ như sau:

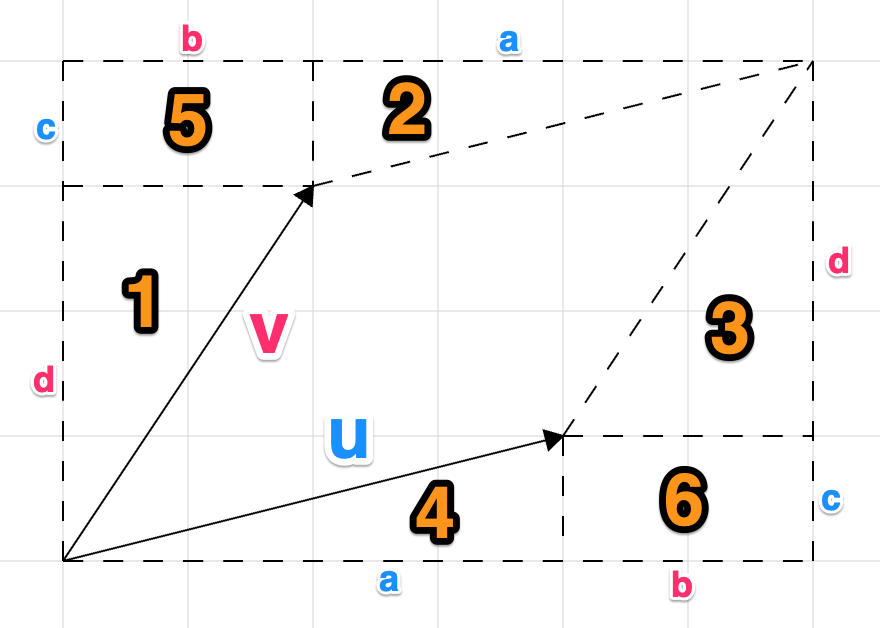
Tức là

$$ \begin{align*} S &= (a+b)(c+d) - \dfrac{1}{2}bd - \dfrac{1}{2}ac - \dfrac{1}{2}bd - \dfrac{1}{2}ac - bc - bc \\ &= (a+b)(c+d) - bd - ac - 2bc \\ &= ac + ad + bc + bd - bd - ac - 2bc \\ &= ad - bc. \end{align*} $$

Trong hình học giải tích, vị trí của vector $u$ và $v$ như hình minh hoạ phía trên được gọi là vị trí thuận, tức là góc quay từ $u$ đến $v$ theo chiều ngược kim đồng hồ là góc nhỏ hơn 180 độ.

Trong trường hợp góc quay đó lớn hơn 180 độ, bạn sẽ thấy nó tương tự như $u$ và $v$ đổi vị trí cho nhau. Dĩ nhiên, các toạ độ và kích thước các cạnh của hình chữ nhật, hình tam giác sẽ không thay đổi, kết quả cuối cùng sẽ là

$$bc-ad.$$

Như vậy, diện tích hình bình hành tạo bởi 2 vector $u$ và $v$ là:

$$|ad-bc|.$$

Mở rộng

Xét ma trận:

$$A = \begin{bmatrix} u\quad v \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix},$$

với $u$ và $v$ là 2 vector cột. Ta có thể nhận ra rằng

$$|A| = ad - bc$$

có giá trị tuyệt đối bằng đúng diện tích hình bình hành tạo bởi hai vector $u$ và $v$. Dấu của $|A|$ cho biết vị trí của hai vector $u$ và $v$ so với nhau. Nếu $|A|$ dương, hai vector $u$ và $v$ nằm ở vị trí thuận, ngược lại nếu $|A|$ âm, hai vector $u$ và $v$ nằm ở vị trí nghịch.

Liệu đây có phải là sự tình cờ?